Geometrie řízení 2

Jelikož je lepší jednou vidět, než 100x slyšet, nosným prvkem článku budou obrázky. Na to, abych mohl demonstrovat různé příklady, bylo nutné bedlivé zvolení figuranta. Jako první byl na ráně samozřejmě inženýr František na "Kejvačce". Řekl mi však, že kvůli vůli v zadní kyvce nemůže pořádně klopit a také mu to moc nebrzdí, protože se mu umazaly pakny od oleje vyteklého z přední vidlice. Druhý byl na ráně švýcarský hoteliér Hugo, původem z Rakouska. Jeho oldtimer je sice pěkně udržován, ale nemá přední teleskopickou vidlici, a pořád jezdí, protože mu nesmí upadnout šál. Takže jsem si nakonec musel vypůjčit Němce Helmuta, který pracuje jako opravář komínů a jeho zánovní japonská vražda z osmdesátých let dokáže ještě pořád rozdovádět nejednu paničku. Jo, a že tyhle pány neznáte? Jen se podívejte na obrázky dolů.

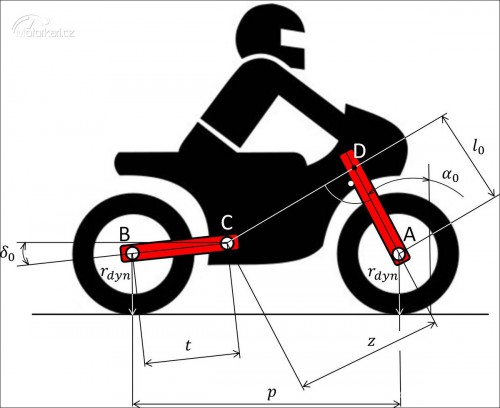
Kompletní geometrie rámu motocyklu je komplexní věc, která nám určuje jeho chování při všech situacích. Kromě známých pojmů, jako je stopa, rozvor a úhel rejdového čepu, zde máme ještě úhel sklonu zadní kyvné vidlice, délku zadní vidlice, dynamický poloměr kola, délku přední vidlice a pomyslnou spojnice osy otáčení zadní kyvné vidlice, kolmou na přední teleskopy. Uvažujeme s konstrukcí, kdy je rovnoběžná osa přední vidlice a rejdového čepu, přední vidlice je teleskopická a zadní kyvná.

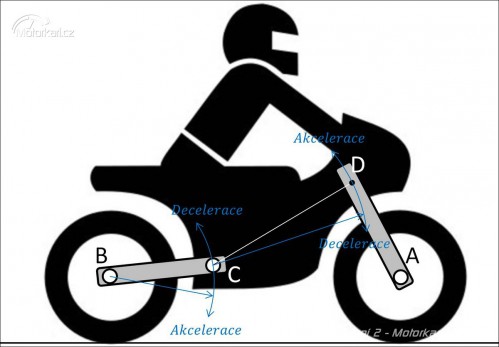
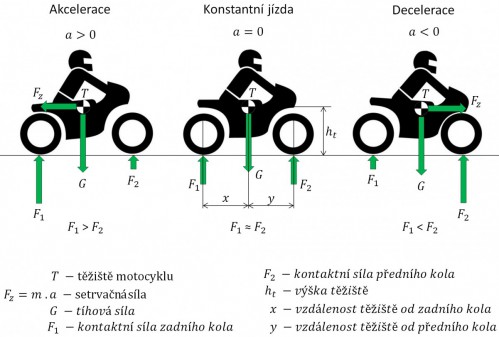
Proč jsou tyhle rozměry důležité, se můžeme podívat na obrázku níže. Ti, kteří sedláte silnější mašiny, než je fichtl, víte, že při akceleraci dochází ke stlačení zadních tlumičů (tlumiče) a vysunutí předních, nebo ke kompletní ztrátě trakce na předním kole vlivem jeho zvednutí. Při brždění pak poznáte ponor přední vidlice i na dobře seřízeném fichtlu. Důsledkem pohybu pružení dochází k pohybu odpružené hmoty motocyklu, v našem případě i s řidičem Helmutem. Šipkami jsou znázorněny pohyby čepů při akceleraci a brždění.

Z obrázku je patrné, že při akceleraci jsou pevnými body pouze osy kol, jež nemění svou relativní polohu vůči vozovce. Ale tohle tvrzení také není úplná pravda, protože se vlivem deformace pneumatiky pod zatížením nepatrně mění i výška os vůči vozovce. O tom, co se děje s pneumatikou, si ukážeme v samostatném článku.

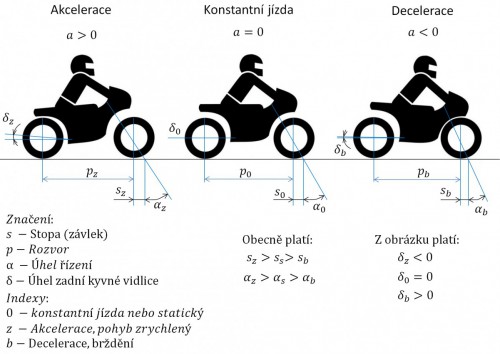
Nemusíme mít vystudovanou fyziku na to, abychom věděli, na kterém zobrazení z obrázku výše se jedná o brždění, konstantní jízdu a zrychlení. Z naší předem definované běžné konstrukce můžeme obecně tvrdit, že stopa při akceleraci bude větší, než statická. Statická stopa je opět větší oproti decelerační. To samé platí o úhlu řízení, protože tyhle veličiny jsou na sobě závislé. Obecně tedy můžeme tvrdit, že je motocykl při brždění méně stabilní vlivem menší stopy. Také je patrná ona změna rozvoru, jehož zvětšení, nebo redukci, určuje poměr a celkové nastavení geometrie přední a zadní nápravy. Stejně tak jsou všechny tyhle veličiny a jejich změny snadno spočítatelné jako goniometrické funkce výše uvedených rozměrů geometrie. Je potřeba připomenout fakt, že nastavení tlumičů hraje v tomhle varieté hlavní roli. Je potřeba, aby přední a zadní tlumič motocyklu měli při jízdě stejnou nebo velice podobnou charakteristiku. Nastavením tlumiče myslím zejména tlumící charakteristiku (tlumení a odskok), také zde ale hraje roli seřízení tuhostí a typů pružin. Tahle veličina se nedá měřit jinak, než na okruhu, a mnohdy je subjektivním pocitem jezdce.

Hmotnost motocyklu se během jízdy nemění, ale na obrázku dole vidíme, že se nějakým způsobem přesouvá. K tomu dochází díky setrvačné síle, která se motocykl snaží udržet v klidu nebo v rovnoměrném pohybu. Tudíž vždy působí proti pohybu, který chceme zrovna vykonat, vyjímaje konstantní jízdy. Co má za následek změnu v rozložení síly mezi koly? Z jednoduché momentové rovnováhy je velice lehké určit poměr zatížení a odlehčení vlivem konkrétního zrychlení.

Jak lze pozorovat na obrázku výše, vlivem pohybu pružení se také mění základní poloha těžiště, tato změna je však minimální a lze ji zanedbat. Samozřejmě, že při jízdě na motocyklu pracuje také jezdec. Správná technika jízdy je taková, že se při brždění posunete směrem k nádrži, abyste byli schopni uvolnit ruce na řídítkách. Při akceleraci je pak znatelný posun těžiště směrem vzad, když se, za stejným účelem, opřete do zadní opěrky. Tahle změna je již na hmotnostních poměrech moderních mašin znatelná. O tom, jak se silové poměry rozloží mezi kola, rozhoduje poloha těžiště definována výškou a rozložením mezi kola v statickém stavu (který se teoreticky neliší od rovnoměrné jízdy).

To, jaká síla působí od kola směrem k vozovce, rozhoduje o trakci. Trakce je v podstatě součinitel tření mezi pneumatikou a vozovkou. Ve škole nám kdysi říkali, že součinitel tření není závislý na ploše a ani na přítlačné síle. Tohle bohužel platí pouze ve fyzice pro školské lavice, kde zanedbáme veškeré všechno (zejména deformaci). V reálném životě (tudíž i skutečné fyzice) platí fakt, že od zatížení je závislá deformace pneumatiky a styčná plocha. Obecně platí pravidlo - čím větší síla tlačí gumu na asfalt, tím větší bude tření (dá se to ověřit třeba na obyčejné gumě). Velikost styčné plochy má přímý vliv na zahřívání pneumatiky a také parciální prokluz, jenž může vést k driftu. Pokud už jste vyzkoušeli širokou paletu motocyklů, tak jste si jistě všimli toho, že sportovní motocykly (například Yamaha R1) mají těžiště posunuté na přední kolo. Naproti tomu enduro má statické těžiště často přesně uprostřed. Naložíte-li své Géeso na dvoutýdenní výlet s baťůžkem, těžiště se vám posouvá směrem vzad a rázem zjistíte, že předek je v ostrých výjezdech poněkud lehký a odskakující.

Regulace trakce pomocí sklonu zadní vidlice - anti-squat geometry.

Helmutův Japonec má samozřejmě převod řešený řetězem. Je to dodnes nejběžnější technické řešení. Mnoho motocyklů prodávaných v dnešní době má v jistém rozsahu možnost seštelování sklonu zadní vidlice. To, jak tahle veličina ovlivňuje trakci, začíná být tématem až s příchodem hodně silných strojů, kdy řešíme mnohem větší hnací síly, nežli kdy předtím. Na obrázku je osa zadního kola označena jako B, čep zadní kyvné vidlice jako C. Zadní Rozeta je číslo 1 a řetězové kolečko je značeno číslem 2. Zobrazeny jsou tři případy sklonu zadní vidlice, přičemž červená šipka znázorňuje vektor hnací síly. Schválně zde neuvádím žádné relevantní silové rozklady ani výpočty, vyobrazení zobrazuje pouze logiku anti-squat geometry.

Je samozřejmě nonsens, aby byla rovně, jak je uvedeno na obrázku, ale takhle je vizuálně jednoduší si představit její pohyb. Tudíž v reálné situaci bude nulový úhel (statický) nenulový. 

Průměr rozety je vlastně páka, za kterou tahá řetěz. Tahle síla je značená červenou šipkou a snaží se otáčet kyvnou vidlicí kolem čepu C. Na obrázku a) je ideální situace, kdy otočení plynové rukojeti transformováno přes řetěz působí onen anti-squat efekt. Zadní vidlice je tlačená směrem k čepu C (působí jeho namáhání) a zároveň se svislá složka síly snaží kolo tlačit směrem k vozovce, tedy vysouvá tlumič pružení. Proti vysouvání tlumiče pak působí setrvačná síla, tedy její vliv na zatížení zadní nápravy. Správným nastavením úhlu tudíž můžeme docílit rovnováhy mezi setrvačnou silou, která zatěžuje tlumič, a kompenzační silou od sekundárního řetězu. To samozřejmě vůbec nemusí fungovat takhle jednoduše, protože setrvačná síla, tudíž i rozložení sil, se mění vlivem zrychlení, a tak je možné rovnovážného nastavení docílit pouze pro jeden konkrétní případ. Při ostatních průjezdech zatáčkou bude mít zadní část motocyklu tendenci zvedat se. Tohle všechno samozřejmě závisí na stylu jízdy, a také na tělesných proporcích jezdce. Zvedání je docela příjemným jevem, kdy je přední kolo přitlačováno k vozovce, a tak kompenzuje potenciální ztrátu trakce. Anti-squat geometry je geometrie, která vylučuje potápění úplně. Na druhém obrázku b) je geometrie, která při prudkém přidání plynu lehce překonává sílu zadního tlumiče a může se dostat do situace z obrázku c), kterou můžeme považovat za mezní situaci při téměř maximálním zrychlení. Modelová situace c) je to nejhorší, co se může stát při výjezdu z apexu. Zadní část je ponořována nejenom rozložením sil, ale také hnací silou. Takže nám hnací síla namáhá přímo tlumič, což má za následek odlehčení předního kola a tak snížení nebo úplnou ztrátu trakce.

Na vybudování správné anti-squat (protiponorné) geometrie je potřeba přesného nastavení odskoku a tlumení zadních a předních tlumičů. Nastavení geometrie zadní vidlice tedy používáme při konečném doladění vzhledem k výkonu motocyklu a stylu jízdy.

Informace o redaktorovi

Marek Janoušek - (Odebírat články autora)
Jiří Jevický - (Odebírat články autora)